Wstęp
Komputerowe wspomaganie projektowania jest w dzisiejszych czasach wykorzystywane w wielu dziedzinach życia. Prawidłowe opanowanie obsługi programów obliczeniowych nie tylko ułatwiają pracę projektanta ale pozwala na szybką analizę bardzo złożonych układów przestrzennych i przyspieszenie pracy. Mając na uwadze te względy zespół 123CAD postanowił przygotować video kurs prezentujący zagadnienia modelowania oraz wymiarowania konstrukcji wykorzystując popularny na rynku europejskim program Autodesk Robot Structural Analysis. Opracowanie to należy traktować jako uzupełnienie do kursu wideo opublikowanego w serwisie internetowym YouTube pod hasłem 123CAD i tytułem „Wymiarowanie Hali stalowej w Autodesk Robot Structural Analysis”. Twórcy w kursie skupiają się na przedstawieniu całego procesu obliczeniowego od zamodelowania konstrukcji, zebrania obciążeń po wymiarowanie i prawidłową interpretację wyników. W odróżnieniu od kursów o podobnej tematyce gdzie prezentowane są pojedyncze zagadnieniach z obsługi programu uważamy, że szczegółowe, krok po kroku przedstawienie problemu pozwoli lepiej go zrozumieć. Opracowanie to ma stanowić integralną część z video kursu a metodyka, przyjęte założenia i wartości obciążeń w ujęciu norm PN-EN zostaną wykorzystane w naszym przykładzie obliczeniowym na łamach serwisu YouTube. To opracowanie jest tylko jedną z części która mamy nadzieje w przyszłości ukaże się na naszym kanale. Opracowanie skierowane jest głównie do studentów kierunków technicznych, ale mamy nadzieje, że każdy chcący zacząć swoją przygodę z komputerowym wspomaganiem projektowania znajdzie tu coś dla siebie.
Założenia projektowe
Parametry projektowanej hali
Warunki geometryczne projektowanej hali:

 Rys.1 Geometria projektowanej hali
Rys.1 Geometria projektowanej hali
Założenia materiałowe
W obliczeniach zostaną wykonane dwa warianty hali:
1. Wariant z płatwiami zimno giętymi których materiał to S350GD +Z
2. Wariant z płatwiami walcowanymi materiał S235
Głowna konstrukcja nośna stal S235
Założenia lokalizacyjne
Nasza projektowana hala znajduje się w II Strefie obciążenia śniegiem oraz w II strefie obciążenia wiatrem.
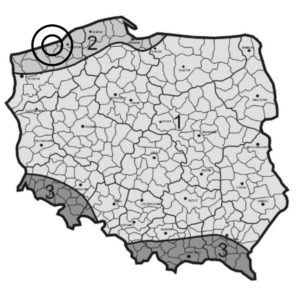 Rys.2 Podział Polski na strefy wiatrowe wg normy PN-EN 1991-1-4:2008
Rys.2 Podział Polski na strefy wiatrowe wg normy PN-EN 1991-1-4:2008
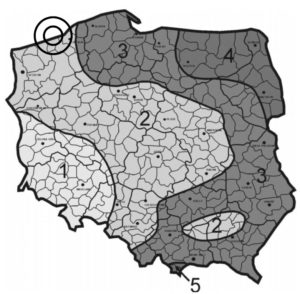 Rys 3. Podział Polski na strefy śniegowe wg normy PN-EN 1991-1-3:2002
Rys 3. Podział Polski na strefy śniegowe wg normy PN-EN 1991-1-3:2002
Przyjęto, że budynek znajduje się w III kategorii terenu zgodnie z tabelą 1
 Tabela 1. Kategorie terenu wg normy PN-EN 1991-1-4 – Tablica 4.1
Tabela 1. Kategorie terenu wg normy PN-EN 1991-1-4 – Tablica 4.1
Ze względu na nachylenie połaci dachu α = 4,8° należy przyjąć, ze dla
oddziaływania wiatru i śniegu ten dach jest dachem płaskim zgodnie z zapisem 7.2.3 normy PN EN 1991-1-4. Budynek jest nieocieplony i nieogrzewany.
Obciążenia
Ciężar własny i obciążenia stałe wg PN-EN 1991-1-1
W normie PN-EN 1991-1-1 zawarto szczegółowe informacje na temat ciężarów objętościowych materiałów budowlanych oraz wartości charakterystyczne obciążeń użytkowych stropów i dachów. Na obciążenia stałe składają się ciężar własny wszystkich elementów konstrukcji hali jak: ramy, płatwie, pokrycie dachowe, pokrycie ścian, świetliki itd. Jako pokrycie dachu oraz ścian w naszym przykładzie obliczeniowym przyjęto blachę trapezową T40 której ciężar własny (charakterystyczny) to 0,067 kN/m2. Dla ścian projektowanej hali przyjęto zastosowanie paneli typu
sandwich których ciężar własny wynosi 0,0595 kN/m2. Dla liczonej hali stalowej nie przyjmujemy obciążeń użytkowych zakładamy, ze dach hali nie jest użytkowany.
Ciężar własny elementów konstrukcyjnych zostanie nadany automatycznie w programie obliczeniowym Autodesk Robot Structural Analysis uwzględniając wykorzystane przekroje w modelu obliczeniowym i ciężar właściwy stali 77,00 kN/m3
Powierzchniowy ciężar stały poszycia dachu i elewacji (charakterystyczny)
Blacha trapezowa T40 – ciężar własny 0,067 kN/m2
G k, 1 = 0,067 kN/m2
Panele elewacyjne sandwich – ciężar własny 0,0595 kN/m2
G k, 2 = 0,0595 kN/m2
Obciążenie śniegiem wg PN-EN 1991-1-3:2002
Obciążenie śniegiem wyznaczamy na podstawie wzoru:
Qk,s = Sk ∙ Ce ∙ Ct ∙ μ1
Gdzie:
Sk – Wartość charakterystyczna obciążenia śniegiem gruntu kN/m2
Ce – Współczynnik ekspozycji
Ct – Współczynnik termiczny
μ1 – Współczynnik kształtu dachu
Projektowana hala znajduje się na pomorzu Polski i jest w II strefie śniegowej zgodnie z rysunkiem 3. Powierzchniowe obciążenie śniegiem gruntu, wartość charakterystyczna dla II strefy śniegowej zgodnie z tabelą 2 wynosi:
Sk = 0,9 [kN/m2]
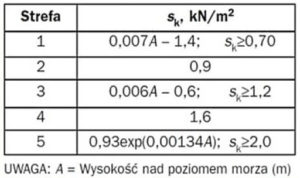
Tabela 2. Powierzchniowe obciążenie śniegiem gruntu wg normy PN-EN 1991-1-3
Kolejnym elementem niezbędnym do wyznaczenia obciążeń śniegiem jest
wyznaczenie współczynnika termicznego, współczynnika ekspozycji oraz
współczynnika kształtu dachu dla kąta nachylenia α = 4,8°
Współczynnik termiczny
Do oceny zmniejszenia obciążenia śniegiem dachów o współczynniku
przenikania ciepła (>1W/m2K) w szczególności niektórych dachów krytych szkłem z powodu topnienia śniegu przez przechodzące ciepło korzystamy ze wzoru NB 1.8. Dla pozostałych przypadków stosować współczynnik termiczny Ct = 1. Stosowanie współczynnika Ct < 1 należy starannie rozważyć.
Ct = 1
Współczynnik ekspozycji
Ce= 1
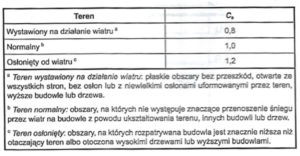
Tabela 3. Zalecane wartości Ce dla różnych warunków terenowych wg normy PN-EN 1991-1-3:200
Współczynnik kształtu dachu dla α = 4,8°
μ1= 0,8
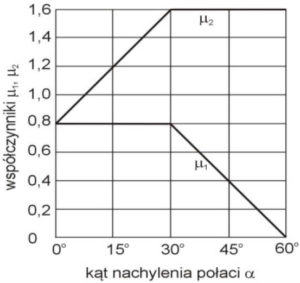
Rys 4. Diagram prezentujący zależność kąta nachylenia połaci dachu do
współczynnika kształtu dachu
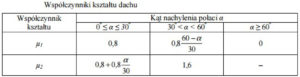
Tabela 4. Współczynnik kształtu dachu uzależniony od kąta nachylenia połaci wg normy PN-EN 1991-1-3:200
Powierzchniowe obciążenie śniegiem połaci hali
Qk,s = Sk ∙ Ce ∙ Ct ∙ μ1 = 0,9 · 1 · 1 · 0.8 = 0.72 kN/m2
Gk,s = 0,72 kN/m2
Obciążenie wiatrem wg PN-EN 1991-1-4
Obciążenie wiatrem będziemy wyznaczać ze wzoru 5.1 z rozdziału 5.2 normy PN-EN 1991-1-4
Qk,w,i = qp(Z) ∙ ( Cpe,10 − Cpi )
Gdzie :
qp(Z) − Wartość charakterystyczna szczytowego ciśnienia prędkości wiatru wg 4.8
Cpe,10 – Współczynnik ciśnienie zewnętrznego
Cpi – Współczynnik ciśnienie wewnętrznego roz. 3.3.4
Qk,w,i – możne przyjąć oznaczenia w zależności od kierunku działania wiatru ∶
Wiatr W1 Qk,w,1 ( θ = 0° )
Wiatr W2 Qk,w,2 ( θ = 90° )
Wiatr W3 Qk,w,3 ( θ = 0° )
Wiatr W4 Qk,w,4 ( θ = 90° )
Zaczniemy od wyznaczenia qp(Z) tj. wartości charakterystycznej szczytowego ciśnienia prędkości wiatru ze wzoru :
qp(Z) =1/2 [ 1 + 7 · Iν(Z)] ρ · νm2
wzór 4.8 wg normy
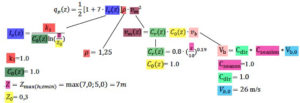
Rys 5. Schemat wyznaczenia elementów składowych qp(z) – opis w tekście
Wzór na qp(z) zawiera wiele składowych które wyznaczymy krok po kroku. Nasza projektowana hala znajduje się w II strefie obciążenia wiatrem zgodnie z rysunkiem 1. Wartość podstawowa bazowej prędkości wiatru zgodnie z tabelą 5.
Vb,0 = 26 m/s
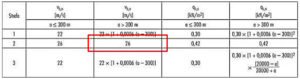 Tabela 5. Wartości podstawowej bazowej prędkości wiatru. Tablica NA1. PN-EN 1991-1-4
Tabela 5. Wartości podstawowej bazowej prędkości wiatru. Tablica NA1. PN-EN 1991-1-4
Współczynnik kierunkowy zgodnie z punktem normy 4.2 oraz uwagą 2 zaleca się stosowanie współczynnika o wartości 1.0
Cdir = 1.0
Współczynnik sezonowy zgodnie z uwagą 3 w rozdziale 4.2 zaleca się stosowanie współczynnika 1.0
Cseason = 1.0
Bazowa prędkość wiatru:
Vb = Cdir ∗ Cseason ∗ Vb,0
Vb = 26 m/s
Wymiar chropowatości terenu Z0 = 0,3
Wysokość minimalna Zmin = 5 m
Na podstawie wzoru 7.2.2 budynek dla którego wysokość h jest mniejsza niż szerokość budynku B, należy traktować jako jedną część o wysokości odniesienia.
Wysokość maksymalna Z = Zmax(h;zmin) = max (7,0 ; 5,0) = 7m
Współczynnik turbulencji k1 = 1.0 – zalecana wartość zgodnie z pkt. 4.7
Współczynnik rzeźby terenu C0(Z) = 1.0 – zalecana wartość zgodnie z pkt. 4.3.1.
Intensywność turbulencji obliczamy ze wzoru 4.7 :
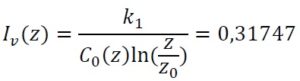
Gdzie:
k1 – współczynnik turbulencji
Co(z) – współczynnik rzeźby terenu
z0 – wymiar chropowatości wg tablicy 4.1 normy PN-EN 1991-1-4. Ze względu na III
kategorię terenu z0 = 0,3.
Współczynnik chropowatości obliczamy ze wzoru:
Cr(Z) = 0.8 ∙ ( z/10)0,19 = 0,74758
Średnia prędkości wiatru:
νm(z) = Cr(Z) · C0(Z) · νb = 19,4371
Wartość charakterystyczna szczytowego ciśnienia prędkości wiatru wg wzoru 4.8:
Podstawiamy do wzoru wszystkie wcześniej wyznaczone wartości i otrzymujemy:
qp(Z) =1/2 [ 1 + 7 · Iν(Z)] ρ · νm2 = 760,87 N/m2 = 0,76 kN/m2
Gdzie:
ρ − gęstość powietrza zależna od wysokości nad poziomem morza,
temperatury i ciśnienia atmosferycznego.
ρ = 1,25
Dla potrzeb przykładu obliczeniowego dokonano podziału wyznaczania
obciążeń dla ścian hali, kierunku wiatru θ=0° oraz θ=90° a następnie dla dachu z kierunku θ=0°oraz θ=90°. Na końcu przedstawiono tabelaryczne zestawienie wartości wszystkich obciążeń dla ścian i dachu łącznie które następnie wykorzystano do obciążenia modelu obliczeniowego w programie Robot.
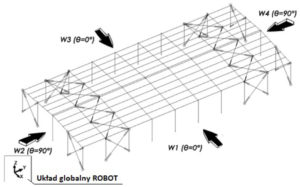
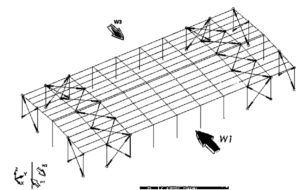
Rys 6. Schemat prezentujący kierunki działania wiatru W1- W4 dla ścian i dachu projektowanej hali.
Objaśnienie oznaczeń:
W1 oznacza wiatr z kierunku θ=0° obciążenie nim wywołane jest zgodne ze zwrotem –X układu globalnego w programie Robot.
W2 oznacza wiatr z kierunku θ=90° obciążenie nim wywołane jest zgodne ze zwrotem Y układu globalnego w programie Robot.
W3 oznacza wiatr z kierunku θ=0° obciążenie nim wywołane jest zgodne ze zwrotem X układu globalnego w programie Robot.
W4 oznacza wiatr z kierunku θ=90° obciążenie nim wywołane jest zgodne ze zwrotem -Y układu globalnego w programie Robot.
Schemat wyznaczenia obciążeń wiatrem W1 i W3 na ściany projektowanej hali z kierunku θ=0°
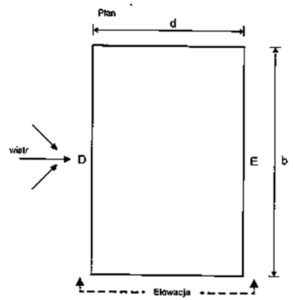
Rys 7. Schematyczny rzut budynku prezentujący oznaczenie ścian dla wiatru W1, W3 θ=0°
Podstawiając odpowiednie parametry naszej projektowanej hali pod oznaczenia z rysunku 7 otrzymujemy:
d = 24m -szerokość ram w osiach
b = 54m – długość budynku
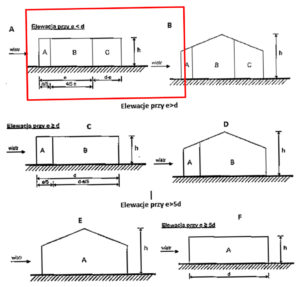
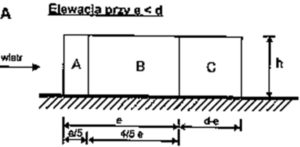
Z wyżej przedstawionego schematu wynika, że nasz wiatr W1 z kierunku θ=0° działa na ścianę D, E oraz na ściany boczne d naszej hali (nazywanej elewacją). Nasza ściana elewacja powinna zostać podzielona na mniejsze pola zgodnie ze schematami z rysunku 8.
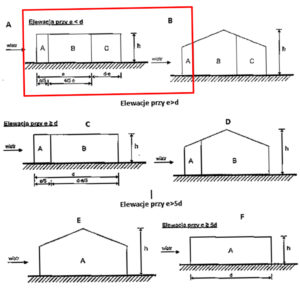
Rys 8. Warianty podziału ściany elewacyjnej dla wiatru W1; W3 θ=0°
Aby wybrać prawidłowy wariant elewacji należy wyznaczyć parametr e gdzie jest on wartością mniejszą z dwóch:

Gdzie:
b – wymiar poprzeczny do kierunku wiatru b = 54m
h – wysokość konstrukcji = 7m
e = 2h = 14m – wartość mniejsza
Kolejnym krokiem jest sprawdzenie wartości parametru d czyli długości ściany bocznej. Dla naszej projektowanej hali d = 24m
Pozostaje określić zależność tych dwóch parametrów:
e < d ; 14m < 24m
W związku z tym, że dach naszej hali (ze względu na spadki dachu) przyjęto jako dach płaski a e<d wariantem podziału naszej ściany bocznej będzie opcja A z rysunku 8.
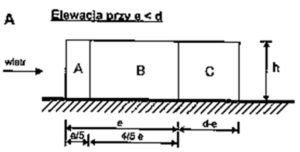
Rys 9. Prawidłowy wariant podziału ściany elewacyjnej dla Wiatru W1; W3 θ=0°- dach płaski
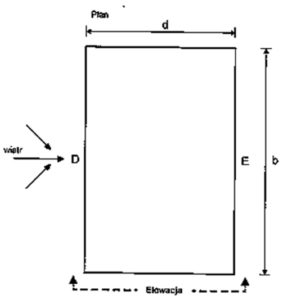
Rys 10. Oznaczanie pozostałych ścian budynku dla wiatru W1; W3 θ=0°
Łącznie nasza projektowana hala została podzielona na 5 pól oddziaływania wiatru na ściany dla Wiatru θ=0*. Ich lokalizację zaprezentowano na rysunku nr 11.

Rys.11 Schematyczna prezentacja podziału ścian dla kierunku wiatru W1;W3 θ=0°
UWAGA: Schemat podziału ściany elewacyjnej d dla kierunku W3 jest
odbiciem lustrzanym podziału W1 tj. Dla kierunku W1 pierwszym polem podziału ściany elewacyjnej jest pole A i tak samo dla kierunku wiatru W3.
Kolejnym krokiem jest określenie zakresów poszczególnych pól. Wartości dla wiatru W1 θ=0° zestawiono w tabeli 6.
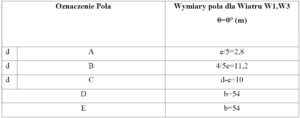
Tabela 6. Zestawienie tabelaryczne oznaczeń poła oraz ich wymiarów (patrz rysunek 9)
Gdzie:
e = 14m
d = 24m
b = 54m
W celu wyznaczenia współczynnika ciśnienia zewnętrznego na ściany
konieczne jest skorzystanie z tabeli nr 7
h/d = 0,29

Tabela 7. Zalecane wartości współczynnika ciśnienia zewnętrznego dla ścian pionowych budynków na rzucie prostokąta
Współczynniki ciśnienie zewnętrznego Cpe,10 dobieramy z tabeli 7 dokonując interpolacji liniowej.
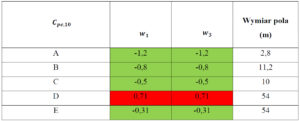
Tabela 8.Współczynnik ciśnienia zewnętrznego na ściany Wiatr W1,W3 θ=0°
Legenda do tabeli 8:
Parcie – skierowane ku powierzchni jest przyjmowane jako dodatnie,
Ssanie – skierowane od powierzchni jako ujemne
W1 oznacza wiatr dla kierunku θ=0° zgodny ze zwrotem –X układu globalnego w programie robot.
W3 oznacza wiatr dla kierunku θ=0° zgodny ze zwrotem +X układu globalnego w programie robot (patrz rysunek 10)
Rys.10 W1 i W3 dla kierunku wiatru θ=0°
UWAGA – Wartości współczynnika ciśnienia zewnętrznego Cpe,10 dla wiatru W3 są identyczne jak dla wiatru W1. Obciążenie wiatrem W3 zostanie przyłożone do modelu obliczeniowego z przeciwnym zwrotem w stosunku do W1.
Schemat wyznaczenia obciążeń wiatrem W2, W4 na ściany projektowanej hali w kierunku θ=90°

Rys 11. Schematyczny rzut budynku prezentujący oznaczenie ścian dla wiatru W2, W4 θ=90°
Podstawiając odpowiednie parametry naszej projektowanej hali pod oznaczenia z rysunku 11 otrzymujemy:
d = 54m – długość budynku
b = 24m – szerokość ram w osiach
Z wyżej przedstawionego rysunku wynika, że nasz wiatr z kierunku θ=90°
działa na ścianę D, E oraz na ściany boczne naszej hali (nazywanej elewacją). Nasza ściana elewacja powinna zostać podzielona na mniejsze pola zgodnie ze schematami z rysunku 12.
Rys 12. Warianty podziału ściany elewacyjnej dla kierunku θ=90°
Aby wybrać prawidłowy wariant elewacji należy wyznaczyć parametr e
jest wartością mniejszą z dwóch:
 Gdzie:
Gdzie:
b – wymiar poprzeczny do kierunku wiatru b = 24m
h – wysokość konstrukcji = 7m
e = 2h = 14m
Kolejnym krokiem jest sprawdzenie wartości parametru d czyli długości ściany bocznej. Dla naszej projektowanej hali d = 54m
Pozostaje określić zależność tych dwóch parametrów:
e < d
W związku z tym, że dach naszej hali (ze względu na spadki dachu) przyjęto jako dach płaski a e < d wariantem podziału naszej ściany bocznej będzie opcja A
Rys 13. Warianty podziału ściany elewacyjnej dla wiatru W2; W4 θ=90°
Wraz z pozostałymi ścianami zgodnie z rysunkiem 1

Rys 14: Oznaczanie pozostałych ścian budynku dla kierunku θ=90°
Łącznie nasza projektowana hala została podzielona na 5 pól oddziaływania wiatru na ściany dla kierunku θ=90*

Rys.15 Schematyczna prezentacja podziału ścian dla kierunku wiatru W2;W4 θ=0°
UWAGA: Schemat podziału ściany elewacyjnej d dla kierunku W4 jest
odbiciem lustrzanym podziału W2 tj. Dla kierunku W2 pierwszym polem podziału ściany elewacyjnej jest pole A i tak samo dla kierunku wiatru W4.
Kolejnym krokiem jest określenie zakresów poszczególnych pól. Wartości dla wiatru W2,W4 θ=0° zestawiono w tabeli 9.
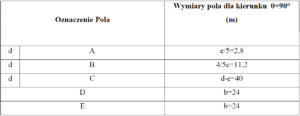
Tabela 9. Zestawienie tabelaryczne oznaczeń poła oraz ich wymiarów
W celu wyznaczenia współczynnika ciśnienia zewnętrznego na ściany
konieczne jest skorzystanie z tabeli nr 9
h/d = 0,13

Tabela 9. Zalecane wartości współczynnika ciśnienia zewnętrznego dla ścian pionowych budynków na rzucie prostokąta
Współczynniki ciśnienie zewnętrznego Cpe,10 dobieramy z tabeli 7 dokonując interpolacji liniowej.
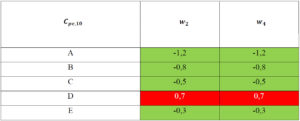
Tabela 10.Współczynnik ciśnienia zewnętrznego na ściany Wiatr W2,W4 θ=90°
Legenda do tabeli 10:
Parcie – skierowane ku powierzchni jest przyjmowane jako dodatnie,
Ssanie – skierowane od powierzchni jako ujemne
W2 oznacza wiatr dla kierunku θ=90° zgodny ze zwrotem +Y układu globalnego w programie robot W4 oznacza wiatr dla kierunku θ=90° zgodny ze zwrotem -Y układu globalnego w programie robot
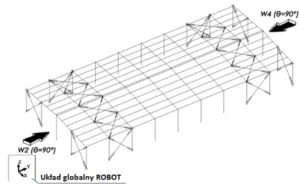
Rys.16 W2 i W4 dla kierunku wiatru θ=90°
Schemat wyznaczenia obciążeń wiatrem W1, W3 na dach projektowanej hali w kierunku θ=0°
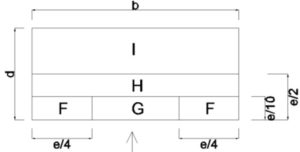
Rys.17 Przyjęty podział dachu hali dla wiatru W1 i W3 dla kierunku θ=0°

Rys.18 Przyjęty podział dachu hali dla wiatru W1 i W3 dla kierunku θ=0° wg normy PN-EN
Pierwszym krokiem jest określenie zakresów poszczególnych pól. Wartości dla kierunku θ=0° zestawiono w tabeli 11
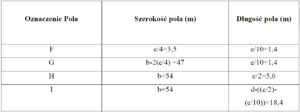
Tabela 11. Zestawienie tabelaryczne oznaczeń poła oraz ich wymiarów
W tabeli 12 możemy zauważyć dwa rodzaje współczynników ciśnienia
zewnętrznego Cpe,10 oraz Cpe,1. Współczynnik Cpe,10 jest podany dla powierzchni konstrukcji o polu powierzchni A = 10m2 ,a Cpe,1 jest współczynnikiem dla konstrukcji o powierzchni A = 1m2. Wartości Cpe,1 są przeznaczone wyłącznie do obliczeń elementów małych łączników o powierzchni elementów 1m2 i mniejszych takich jak elementy
ścian osłonowych i dachów. W przypadku naszej projektowanej hali mamy do czynienia ze współczynnikiem Cpe,10 do obliczeń konstrukcji nośnych budynków jako całości. W przypadku naszej hali mamy do czynienia z dachem o ostrych krawędziach.
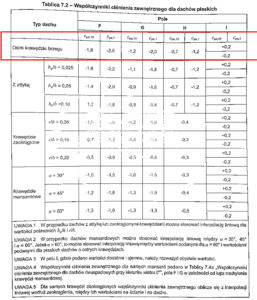
Tabela 12. Zestawienie ciśnienia zewnętrznego dla dachów płaskich
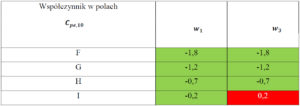
Tabela 13.Współczynnik ciśnienia zewnętrznego dla dachu kierunek θ=0° wg tabeli 12
Schemat wyznaczenia obciążeń wiatrem W2 i W4 na dach projektowanej hali w kierunku θ=90°
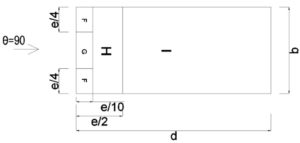
Rys.19 Przyjęty podział dachu hali dla wiatru W2 i W4 dla kierunku θ=90°
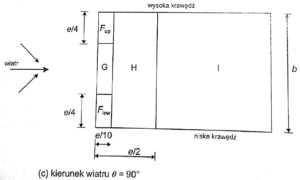
Rys.20 Przyjęty podział dachu hali dla wiatru W2 i W4 dla kierunku θ=90° wg normy PN-EN
Pierwszym krokiem jest określenie zakresów poszczególnych pól. Wartości dla kierunku θ=90° zestawiono w tabeli 11

Tabela 14. Zestawienie tabelaryczne oznaczeń poła oraz ich wymiarów
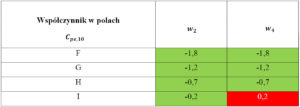
Tabela 15.Współczynnik ciśnienia zewnętrznego dla dachu kierunek θ=90° wg tabeli 12
Dla projektowanej hali należy przyjąć również dwie wartości współczynników
ciśnienia wewnętrznego Cpi odpowiadające odpowiednio nadciśnieniu Cpi = +0,2 oraz podciśnieniu w budynku Cpi = – 0,3. Różnica współczynnika ciśnienia zewnętrznego i wewnętrznego jest najbardziej niekorzystna. Wartości współczynnika ciśnienia wewnętrznego należy określić na podstawie diagramu zgodnie z uwagą 6 w rozdziale 7.2.9 normy (3) uwzględniając współczynnik przepuszczalności przegrody μ.
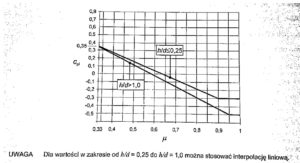
Rys 21. Wartość Cpi w zależności od współczynnika μ
Stosując się do uwagi 2 w rozdziale 7.2.9 w sytuacji gdy określenie μ jest nie możliwe lub nie jest uważane za uzasadnione wówczas należy przyjąć bardziej niekorzystną wartość z dwóch:
a) Cpi = +0,2
b) Cpi = – 0,3

Rys 22. Graficzna prezentacja działania współczynnika ciśnienia wewnętrznego
a) Parcie skierowane ku powierzchni jest przyjmowane jako dodatnie
b) Ssanie skierowane od powierzchni jest przyjmowane jako ujemne
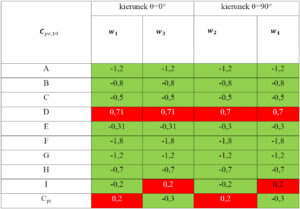
Tabela 16. Łączne zestawienie współczynnika ciśnienia zewnętrznego Cpe,10 oraz wewnętrznego Cpi dla dachu oraz ścian hali kierunek θ=0° oraz θ=90°
Ostateczne wartości obciążeń wiatrem dla wszystkich kierunków działania wiatru.
Obciążenie wiatrem na projektowaną halę należy obliczyć ze wzory 5.1 w
rozdziale 5.2 normy PN EN 1991-1-4
Qk,w,i = qp(Z) ∙ ( Cpe,10 − Cpi )
qp(Z) − Wartość charakterystyczna szczytowego ciśnienia prędkości wiatru wg 4.8
Cpe,10 – Współczynnik ciśnienie zewnętrznego
Cpi – Współczynnik ciśnienie wewnętrznego
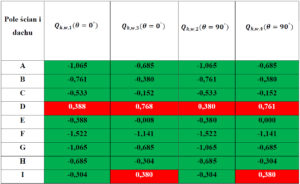
Tabela 17. Łączne zestawienie obciążeń dla dachu oraz ścian hali kierunek θ=0° oraz θ=90° wyrażone w [kN/m2]
Przykład podstawienia do wzoru:
Obciążenie wiatrem W1 pola A
Qk,w,1 (θ = 0°) = qp(z) ∙ (Cpe,10 − Cpi) = 0,76 kN/m2 · (-1,2 – 0,2) = -1,065 kN/m2
Obciążenie wiatrem W3 pola I
Qk,w,3 (θ = 0°) = qp(z) ∙ (Cpe,10 − Cpi) = 0,76 kN/m2 · (0,2 + 0,3) = 0,380 kN/m2

Rys 23. Graficzna prezentacja przyłożenia obciążeń na model projektowanej hali dla wiatru W1 θ=0° i W2 θ=90° (wiatr W3 oraz W4 analogicznie)
Obciążenia na budynek hali w ujęciu norm Eurokod. Modelowanie obciążeń w programie Autodesk Robot Structural Analysis
Wstęp
Komputerowe wspomaganie projektowania jest w dzisiejszych czasach wykorzystywane w wielu dziedzinach życia. Prawidłowe opanowanie obsługi programów obliczeniowych nie tylko ułatwiają pracę projektanta ale pozwala na szybką analizę bardzo złożonych układów przestrzennych i przyspieszenie pracy. Mając na uwadze te względy zespół 123CAD postanowił przygotować video kurs prezentujący zagadnienia modelowania oraz wymiarowania konstrukcji wykorzystując popularny na rynku europejskim program Autodesk Robot Structural Analysis. Opracowanie to należy traktować jako uzupełnienie do kursu wideo opublikowanego w serwisie internetowym YouTube pod hasłem 123CAD i tytułem „Wymiarowanie Hali stalowej w Autodesk Robot Structural Analysis”. Twórcy w kursie skupiają się na przedstawieniu całego procesu obliczeniowego od zamodelowania konstrukcji, zebrania obciążeń po wymiarowanie i prawidłową interpretację wyników. W odróżnieniu od kursów o podobnej tematyce gdzie prezentowane są pojedyncze zagadnieniach z obsługi programu uważamy, że szczegółowe, krok po kroku przedstawienie problemu pozwoli lepiej go zrozumieć. Opracowanie to ma stanowić integralną część z video kursu a metodyka, przyjęte założenia i wartości obciążeń w ujęciu norm PN-EN zostaną wykorzystane w naszym przykładzie obliczeniowym na łamach serwisu YouTube. To opracowanie jest tylko jedną z części która mamy nadzieje w przyszłości ukaże się na naszym kanale. Opracowanie skierowane jest głównie do studentów kierunków technicznych, ale mamy nadzieje, że każdy chcący zacząć swoją przygodę z komputerowym wspomaganiem projektowania znajdzie tu coś dla siebie.
Założenia projektowe
Parametry projektowanej hali
Warunki geometryczne projektowanej hali:
Założenia materiałowe
W obliczeniach zostaną wykonane dwa warianty hali:
1. Wariant z płatwiami zimno giętymi których materiał to S350GD +Z
2. Wariant z płatwiami walcowanymi materiał S235
Głowna konstrukcja nośna stal S235
Założenia lokalizacyjne
Nasza projektowana hala znajduje się w II Strefie obciążenia śniegiem oraz w II strefie obciążenia wiatrem.
Przyjęto, że budynek znajduje się w III kategorii terenu zgodnie z tabelą 1
Ze względu na nachylenie połaci dachu α = 4,8° należy przyjąć, ze dla
oddziaływania wiatru i śniegu ten dach jest dachem płaskim zgodnie z zapisem 7.2.3 normy PN EN 1991-1-4. Budynek jest nieocieplony i nieogrzewany.
Obciążenia
Ciężar własny i obciążenia stałe wg PN-EN 1991-1-1
W normie PN-EN 1991-1-1 zawarto szczegółowe informacje na temat ciężarów objętościowych materiałów budowlanych oraz wartości charakterystyczne obciążeń użytkowych stropów i dachów. Na obciążenia stałe składają się ciężar własny wszystkich elementów konstrukcji hali jak: ramy, płatwie, pokrycie dachowe, pokrycie ścian, świetliki itd. Jako pokrycie dachu oraz ścian w naszym przykładzie obliczeniowym przyjęto blachę trapezową T40 której ciężar własny (charakterystyczny) to 0,067 kN/m2. Dla ścian projektowanej hali przyjęto zastosowanie paneli typu
sandwich których ciężar własny wynosi 0,0595 kN/m2. Dla liczonej hali stalowej nie przyjmujemy obciążeń użytkowych zakładamy, ze dach hali nie jest użytkowany.
Ciężar własny elementów konstrukcyjnych zostanie nadany automatycznie w programie obliczeniowym Autodesk Robot Structural Analysis uwzględniając wykorzystane przekroje w modelu obliczeniowym i ciężar właściwy stali 77,00 kN/m3
Powierzchniowy ciężar stały poszycia dachu i elewacji (charakterystyczny)
Blacha trapezowa T40 – ciężar własny 0,067 kN/m2
G k, 1 = 0,067 kN/m2
Panele elewacyjne sandwich – ciężar własny 0,0595 kN/m2
G k, 2 = 0,0595 kN/m2
Obciążenie śniegiem wg PN-EN 1991-1-3:2002
Obciążenie śniegiem wyznaczamy na podstawie wzoru:
Qk,s = Sk ∙ Ce ∙ Ct ∙ μ1
Gdzie:
Sk – Wartość charakterystyczna obciążenia śniegiem gruntu kN/m2
Ce – Współczynnik ekspozycji
Ct – Współczynnik termiczny
μ1 – Współczynnik kształtu dachu
Projektowana hala znajduje się na pomorzu Polski i jest w II strefie śniegowej zgodnie z rysunkiem 3. Powierzchniowe obciążenie śniegiem gruntu, wartość charakterystyczna dla II strefy śniegowej zgodnie z tabelą 2 wynosi:
Sk = 0,9 [kN/m2]
Tabela 2. Powierzchniowe obciążenie śniegiem gruntu wg normy PN-EN 1991-1-3
Kolejnym elementem niezbędnym do wyznaczenia obciążeń śniegiem jest
wyznaczenie współczynnika termicznego, współczynnika ekspozycji oraz
współczynnika kształtu dachu dla kąta nachylenia α = 4,8°
Współczynnik termiczny
Do oceny zmniejszenia obciążenia śniegiem dachów o współczynniku
przenikania ciepła (>1W/m2K) w szczególności niektórych dachów krytych szkłem z powodu topnienia śniegu przez przechodzące ciepło korzystamy ze wzoru NB 1.8. Dla pozostałych przypadków stosować współczynnik termiczny Ct = 1. Stosowanie współczynnika Ct < 1 należy starannie rozważyć.
Ct = 1
Współczynnik ekspozycji
Ce= 1

Tabela 3. Zalecane wartości Ce dla różnych warunków terenowych wg normy PN-EN 1991-1-3:200
Współczynnik kształtu dachu dla α = 4,8°
μ1= 0,8
Rys 4. Diagram prezentujący zależność kąta nachylenia połaci dachu do
współczynnika kształtu dachu
Tabela 4. Współczynnik kształtu dachu uzależniony od kąta nachylenia połaci wg normy PN-EN 1991-1-3:200
Powierzchniowe obciążenie śniegiem połaci hali
Qk,s = Sk ∙ Ce ∙ Ct ∙ μ1 = 0,9 · 1 · 1 · 0.8 = 0.72 kN/m2
Gk,s = 0,72 kN/m2
Obciążenie wiatrem wg PN-EN 1991-1-4
Obciążenie wiatrem będziemy wyznaczać ze wzoru 5.1 z rozdziału 5.2 normy PN-EN 1991-1-4
Qk,w,i = qp(Z) ∙ ( Cpe,10 − Cpi )
Gdzie :
qp(Z) − Wartość charakterystyczna szczytowego ciśnienia prędkości wiatru wg 4.8
Cpe,10 – Współczynnik ciśnienie zewnętrznego
Cpi – Współczynnik ciśnienie wewnętrznego roz. 3.3.4
Qk,w,i – możne przyjąć oznaczenia w zależności od kierunku działania wiatru ∶
Wiatr W1 Qk,w,1 ( θ = 0° )
Wiatr W2 Qk,w,2 ( θ = 90° )
Wiatr W3 Qk,w,3 ( θ = 0° )
Wiatr W4 Qk,w,4 ( θ = 90° )
Zaczniemy od wyznaczenia qp(Z) tj. wartości charakterystycznej szczytowego ciśnienia prędkości wiatru ze wzoru :
qp(Z) =1/2 [ 1 + 7 · Iν(Z)] ρ · νm2
wzór 4.8 wg normy
Rys 5. Schemat wyznaczenia elementów składowych qp(z) – opis w tekście
Wzór na qp(z) zawiera wiele składowych które wyznaczymy krok po kroku. Nasza projektowana hala znajduje się w II strefie obciążenia wiatrem zgodnie z rysunkiem 1. Wartość podstawowa bazowej prędkości wiatru zgodnie z tabelą 5.
Vb,0 = 26 m/s
Współczynnik kierunkowy zgodnie z punktem normy 4.2 oraz uwagą 2 zaleca się stosowanie współczynnika o wartości 1.0
Cdir = 1.0
Współczynnik sezonowy zgodnie z uwagą 3 w rozdziale 4.2 zaleca się stosowanie współczynnika 1.0
Cseason = 1.0
Bazowa prędkość wiatru:
Vb = Cdir ∗ Cseason ∗ Vb,0
Vb = 26 m/s
Wymiar chropowatości terenu Z0 = 0,3
Wysokość minimalna Zmin = 5 m
Na podstawie wzoru 7.2.2 budynek dla którego wysokość h jest mniejsza niż szerokość budynku B, należy traktować jako jedną część o wysokości odniesienia.
Wysokość maksymalna Z = Zmax(h;zmin) = max (7,0 ; 5,0) = 7m
Współczynnik turbulencji k1 = 1.0 – zalecana wartość zgodnie z pkt. 4.7
Współczynnik rzeźby terenu C0(Z) = 1.0 – zalecana wartość zgodnie z pkt. 4.3.1.
Intensywność turbulencji obliczamy ze wzoru 4.7 :
Gdzie:
k1 – współczynnik turbulencji
Co(z) – współczynnik rzeźby terenu
z0 – wymiar chropowatości wg tablicy 4.1 normy PN-EN 1991-1-4. Ze względu na III
kategorię terenu z0 = 0,3.
Współczynnik chropowatości obliczamy ze wzoru:
Cr(Z) = 0.8 ∙ ( z/10)0,19 = 0,74758
Średnia prędkości wiatru:
νm(z) = Cr(Z) · C0(Z) · νb = 19,4371
Wartość charakterystyczna szczytowego ciśnienia prędkości wiatru wg wzoru 4.8:
Podstawiamy do wzoru wszystkie wcześniej wyznaczone wartości i otrzymujemy:
qp(Z) =1/2 [ 1 + 7 · Iν(Z)] ρ · νm2 = 760,87 N/m2 = 0,76 kN/m2
Gdzie:
ρ − gęstość powietrza zależna od wysokości nad poziomem morza,
temperatury i ciśnienia atmosferycznego.
ρ = 1,25
Dla potrzeb przykładu obliczeniowego dokonano podziału wyznaczania
obciążeń dla ścian hali, kierunku wiatru θ=0° oraz θ=90° a następnie dla dachu z kierunku θ=0°oraz θ=90°. Na końcu przedstawiono tabelaryczne zestawienie wartości wszystkich obciążeń dla ścian i dachu łącznie które następnie wykorzystano do obciążenia modelu obliczeniowego w programie Robot.
Rys 6. Schemat prezentujący kierunki działania wiatru W1- W4 dla ścian i dachu projektowanej hali.
Objaśnienie oznaczeń:
W1 oznacza wiatr z kierunku θ=0° obciążenie nim wywołane jest zgodne ze zwrotem –X układu globalnego w programie Robot.
W2 oznacza wiatr z kierunku θ=90° obciążenie nim wywołane jest zgodne ze zwrotem Y układu globalnego w programie Robot.
W3 oznacza wiatr z kierunku θ=0° obciążenie nim wywołane jest zgodne ze zwrotem X układu globalnego w programie Robot.
W4 oznacza wiatr z kierunku θ=90° obciążenie nim wywołane jest zgodne ze zwrotem -Y układu globalnego w programie Robot.
Schemat wyznaczenia obciążeń wiatrem W1 i W3 na ściany projektowanej hali z kierunku θ=0°
Rys 7. Schematyczny rzut budynku prezentujący oznaczenie ścian dla wiatru W1, W3 θ=0°
Podstawiając odpowiednie parametry naszej projektowanej hali pod oznaczenia z rysunku 7 otrzymujemy:
d = 24m -szerokość ram w osiach
b = 54m – długość budynku
Z wyżej przedstawionego schematu wynika, że nasz wiatr W1 z kierunku θ=0° działa na ścianę D, E oraz na ściany boczne d naszej hali (nazywanej elewacją). Nasza ściana elewacja powinna zostać podzielona na mniejsze pola zgodnie ze schematami z rysunku 8.
Rys 8. Warianty podziału ściany elewacyjnej dla wiatru W1; W3 θ=0°
Aby wybrać prawidłowy wariant elewacji należy wyznaczyć parametr e gdzie jest on wartością mniejszą z dwóch:
Gdzie:
b – wymiar poprzeczny do kierunku wiatru b = 54m
h – wysokość konstrukcji = 7m
e = 2h = 14m – wartość mniejsza
Kolejnym krokiem jest sprawdzenie wartości parametru d czyli długości ściany bocznej. Dla naszej projektowanej hali d = 24m
Pozostaje określić zależność tych dwóch parametrów:
e < d ; 14m < 24m
W związku z tym, że dach naszej hali (ze względu na spadki dachu) przyjęto jako dach płaski a e<d wariantem podziału naszej ściany bocznej będzie opcja A z rysunku 8.
Rys 9. Prawidłowy wariant podziału ściany elewacyjnej dla Wiatru W1; W3 θ=0°- dach płaski
Rys 10. Oznaczanie pozostałych ścian budynku dla wiatru W1; W3 θ=0°
Łącznie nasza projektowana hala została podzielona na 5 pól oddziaływania wiatru na ściany dla Wiatru θ=0*. Ich lokalizację zaprezentowano na rysunku nr 11.
Rys.11 Schematyczna prezentacja podziału ścian dla kierunku wiatru W1;W3 θ=0°
UWAGA: Schemat podziału ściany elewacyjnej d dla kierunku W3 jest
odbiciem lustrzanym podziału W1 tj. Dla kierunku W1 pierwszym polem podziału ściany elewacyjnej jest pole A i tak samo dla kierunku wiatru W3.
Kolejnym krokiem jest określenie zakresów poszczególnych pól. Wartości dla wiatru W1 θ=0° zestawiono w tabeli 6.
Tabela 6. Zestawienie tabelaryczne oznaczeń poła oraz ich wymiarów (patrz rysunek 9)
Gdzie:
e = 14m
d = 24m
b = 54m
W celu wyznaczenia współczynnika ciśnienia zewnętrznego na ściany
konieczne jest skorzystanie z tabeli nr 7
h/d = 0,29
Tabela 7. Zalecane wartości współczynnika ciśnienia zewnętrznego dla ścian pionowych budynków na rzucie prostokąta
Współczynniki ciśnienie zewnętrznego Cpe,10 dobieramy z tabeli 7 dokonując interpolacji liniowej.
Tabela 8.Współczynnik ciśnienia zewnętrznego na ściany Wiatr W1,W3 θ=0°
Legenda do tabeli 8:
Parcie – skierowane ku powierzchni jest przyjmowane jako dodatnie,
Ssanie – skierowane od powierzchni jako ujemne
W1 oznacza wiatr dla kierunku θ=0° zgodny ze zwrotem –X układu globalnego w programie robot.
W3 oznacza wiatr dla kierunku θ=0° zgodny ze zwrotem +X układu globalnego w programie robot (patrz rysunek 10)
Rys.10 W1 i W3 dla kierunku wiatru θ=0°
UWAGA – Wartości współczynnika ciśnienia zewnętrznego Cpe,10 dla wiatru W3 są identyczne jak dla wiatru W1. Obciążenie wiatrem W3 zostanie przyłożone do modelu obliczeniowego z przeciwnym zwrotem w stosunku do W1.
Schemat wyznaczenia obciążeń wiatrem W2, W4 na ściany projektowanej hali w kierunku θ=90°
Rys 11. Schematyczny rzut budynku prezentujący oznaczenie ścian dla wiatru W2, W4 θ=90°
Podstawiając odpowiednie parametry naszej projektowanej hali pod oznaczenia z rysunku 11 otrzymujemy:
d = 54m – długość budynku
b = 24m – szerokość ram w osiach
Z wyżej przedstawionego rysunku wynika, że nasz wiatr z kierunku θ=90°
działa na ścianę D, E oraz na ściany boczne naszej hali (nazywanej elewacją). Nasza ściana elewacja powinna zostać podzielona na mniejsze pola zgodnie ze schematami z rysunku 12.
Rys 12. Warianty podziału ściany elewacyjnej dla kierunku θ=90°
Aby wybrać prawidłowy wariant elewacji należy wyznaczyć parametr e
jest wartością mniejszą z dwóch:
b – wymiar poprzeczny do kierunku wiatru b = 24m
h – wysokość konstrukcji = 7m
e = 2h = 14m
Kolejnym krokiem jest sprawdzenie wartości parametru d czyli długości ściany bocznej. Dla naszej projektowanej hali d = 54m
Pozostaje określić zależność tych dwóch parametrów:
e < d
W związku z tym, że dach naszej hali (ze względu na spadki dachu) przyjęto jako dach płaski a e < d wariantem podziału naszej ściany bocznej będzie opcja A
Rys 13. Warianty podziału ściany elewacyjnej dla wiatru W2; W4 θ=90°
Wraz z pozostałymi ścianami zgodnie z rysunkiem 1

Rys 14: Oznaczanie pozostałych ścian budynku dla kierunku θ=90°
Łącznie nasza projektowana hala została podzielona na 5 pól oddziaływania wiatru na ściany dla kierunku θ=90*
Rys.15 Schematyczna prezentacja podziału ścian dla kierunku wiatru W2;W4 θ=0°
UWAGA: Schemat podziału ściany elewacyjnej d dla kierunku W4 jest
odbiciem lustrzanym podziału W2 tj. Dla kierunku W2 pierwszym polem podziału ściany elewacyjnej jest pole A i tak samo dla kierunku wiatru W4.
Kolejnym krokiem jest określenie zakresów poszczególnych pól. Wartości dla wiatru W2,W4 θ=0° zestawiono w tabeli 9.
Tabela 9. Zestawienie tabelaryczne oznaczeń poła oraz ich wymiarów
W celu wyznaczenia współczynnika ciśnienia zewnętrznego na ściany
konieczne jest skorzystanie z tabeli nr 9
h/d = 0,13
Tabela 9. Zalecane wartości współczynnika ciśnienia zewnętrznego dla ścian pionowych budynków na rzucie prostokąta
Współczynniki ciśnienie zewnętrznego Cpe,10 dobieramy z tabeli 7 dokonując interpolacji liniowej.
Tabela 10.Współczynnik ciśnienia zewnętrznego na ściany Wiatr W2,W4 θ=90°
Legenda do tabeli 10:
Parcie – skierowane ku powierzchni jest przyjmowane jako dodatnie,
Ssanie – skierowane od powierzchni jako ujemne
W2 oznacza wiatr dla kierunku θ=90° zgodny ze zwrotem +Y układu globalnego w programie robot W4 oznacza wiatr dla kierunku θ=90° zgodny ze zwrotem -Y układu globalnego w programie robot
Rys.16 W2 i W4 dla kierunku wiatru θ=90°
Schemat wyznaczenia obciążeń wiatrem W1, W3 na dach projektowanej hali w kierunku θ=0°
Rys.17 Przyjęty podział dachu hali dla wiatru W1 i W3 dla kierunku θ=0°
Rys.18 Przyjęty podział dachu hali dla wiatru W1 i W3 dla kierunku θ=0° wg normy PN-EN
Pierwszym krokiem jest określenie zakresów poszczególnych pól. Wartości dla kierunku θ=0° zestawiono w tabeli 11
Tabela 11. Zestawienie tabelaryczne oznaczeń poła oraz ich wymiarów
W tabeli 12 możemy zauważyć dwa rodzaje współczynników ciśnienia
zewnętrznego Cpe,10 oraz Cpe,1. Współczynnik Cpe,10 jest podany dla powierzchni konstrukcji o polu powierzchni A = 10m2 ,a Cpe,1 jest współczynnikiem dla konstrukcji o powierzchni A = 1m2. Wartości Cpe,1 są przeznaczone wyłącznie do obliczeń elementów małych łączników o powierzchni elementów 1m2 i mniejszych takich jak elementy
ścian osłonowych i dachów. W przypadku naszej projektowanej hali mamy do czynienia ze współczynnikiem Cpe,10 do obliczeń konstrukcji nośnych budynków jako całości. W przypadku naszej hali mamy do czynienia z dachem o ostrych krawędziach.
Tabela 12. Zestawienie ciśnienia zewnętrznego dla dachów płaskich
Tabela 13.Współczynnik ciśnienia zewnętrznego dla dachu kierunek θ=0° wg tabeli 12
Schemat wyznaczenia obciążeń wiatrem W2 i W4 na dach projektowanej hali w kierunku θ=90°
Rys.19 Przyjęty podział dachu hali dla wiatru W2 i W4 dla kierunku θ=90°
Rys.20 Przyjęty podział dachu hali dla wiatru W2 i W4 dla kierunku θ=90° wg normy PN-EN
Pierwszym krokiem jest określenie zakresów poszczególnych pól. Wartości dla kierunku θ=90° zestawiono w tabeli 11
Tabela 14. Zestawienie tabelaryczne oznaczeń poła oraz ich wymiarów
Tabela 15.Współczynnik ciśnienia zewnętrznego dla dachu kierunek θ=90° wg tabeli 12
Dla projektowanej hali należy przyjąć również dwie wartości współczynników
ciśnienia wewnętrznego Cpi odpowiadające odpowiednio nadciśnieniu Cpi = +0,2 oraz podciśnieniu w budynku Cpi = – 0,3. Różnica współczynnika ciśnienia zewnętrznego i wewnętrznego jest najbardziej niekorzystna. Wartości współczynnika ciśnienia wewnętrznego należy określić na podstawie diagramu zgodnie z uwagą 6 w rozdziale 7.2.9 normy (3) uwzględniając współczynnik przepuszczalności przegrody μ.
Rys 21. Wartość Cpi w zależności od współczynnika μ
Stosując się do uwagi 2 w rozdziale 7.2.9 w sytuacji gdy określenie μ jest nie możliwe lub nie jest uważane za uzasadnione wówczas należy przyjąć bardziej niekorzystną wartość z dwóch:
a) Cpi = +0,2
b) Cpi = – 0,3
Rys 22. Graficzna prezentacja działania współczynnika ciśnienia wewnętrznego
a) Parcie skierowane ku powierzchni jest przyjmowane jako dodatnie
b) Ssanie skierowane od powierzchni jest przyjmowane jako ujemne
Tabela 16. Łączne zestawienie współczynnika ciśnienia zewnętrznego Cpe,10 oraz wewnętrznego Cpi dla dachu oraz ścian hali kierunek θ=0° oraz θ=90°
Ostateczne wartości obciążeń wiatrem dla wszystkich kierunków działania wiatru.
Obciążenie wiatrem na projektowaną halę należy obliczyć ze wzory 5.1 w
rozdziale 5.2 normy PN EN 1991-1-4
Qk,w,i = qp(Z) ∙ ( Cpe,10 − Cpi )
qp(Z) − Wartość charakterystyczna szczytowego ciśnienia prędkości wiatru wg 4.8
Cpe,10 – Współczynnik ciśnienie zewnętrznego
Cpi – Współczynnik ciśnienie wewnętrznego
Tabela 17. Łączne zestawienie obciążeń dla dachu oraz ścian hali kierunek θ=0° oraz θ=90° wyrażone w [kN/m2]
Przykład podstawienia do wzoru:
Obciążenie wiatrem W1 pola A
Qk,w,1 (θ = 0°) = qp(z) ∙ (Cpe,10 − Cpi) = 0,76 kN/m2 · (-1,2 – 0,2) = -1,065 kN/m2
Obciążenie wiatrem W3 pola I
Qk,w,3 (θ = 0°) = qp(z) ∙ (Cpe,10 − Cpi) = 0,76 kN/m2 · (0,2 + 0,3) = 0,380 kN/m2
Rys 23. Graficzna prezentacja przyłożenia obciążeń na model projektowanej hali dla wiatru W1 θ=0° i W2 θ=90° (wiatr W3 oraz W4 analogicznie)
admin